Linear Regression
June 22, 2025
Modeling
- Use models to explore the relationship between variables and to make predictions
- Explaining relationships (usually interested in causal relationships, but not always)
- Does oil wealth impact regime type?
- Predictive modeling
- Where is violence most likely to happen in (country X) during their next election?
- Is this email spam?
Modeling
Modeling
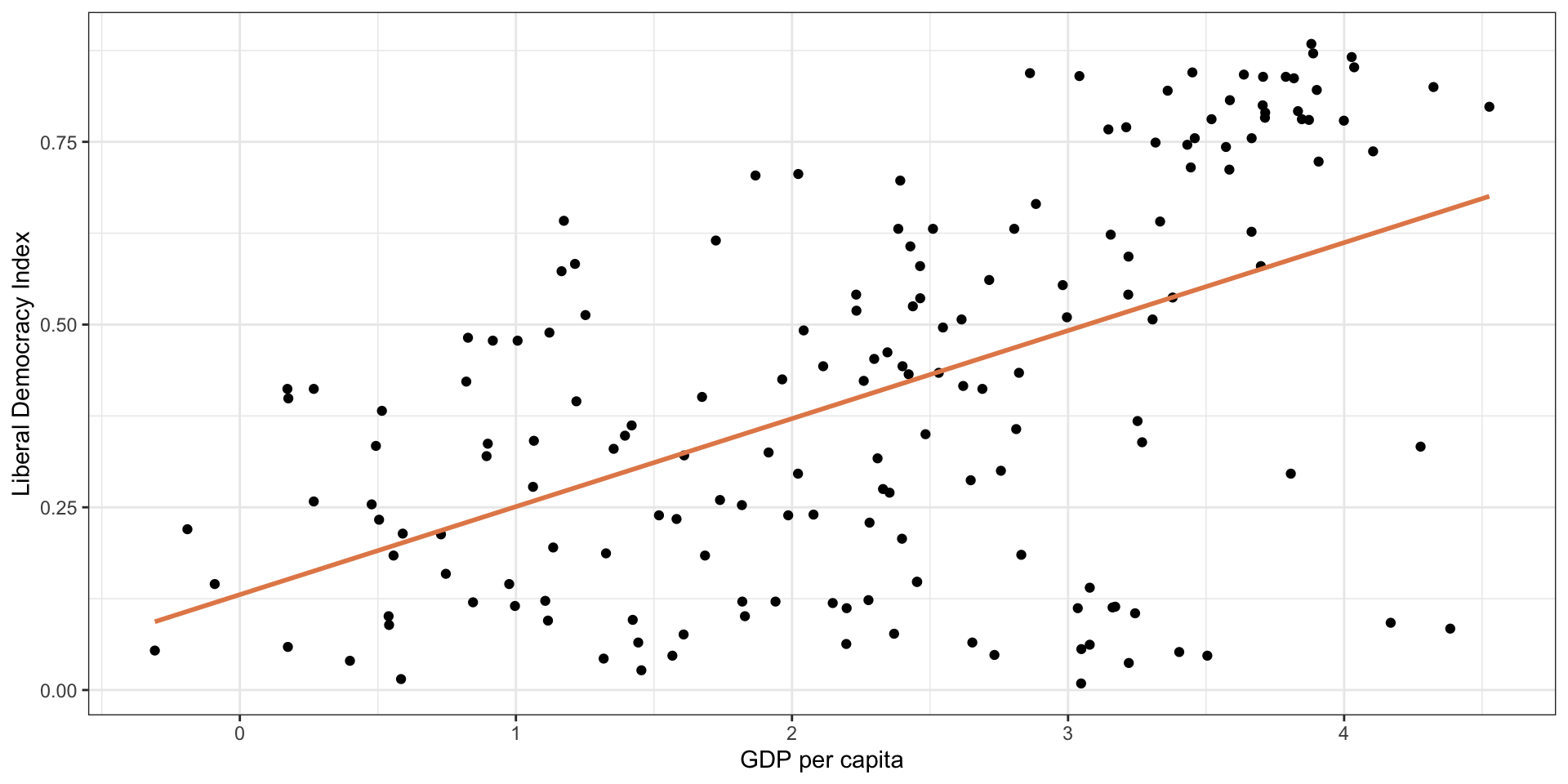
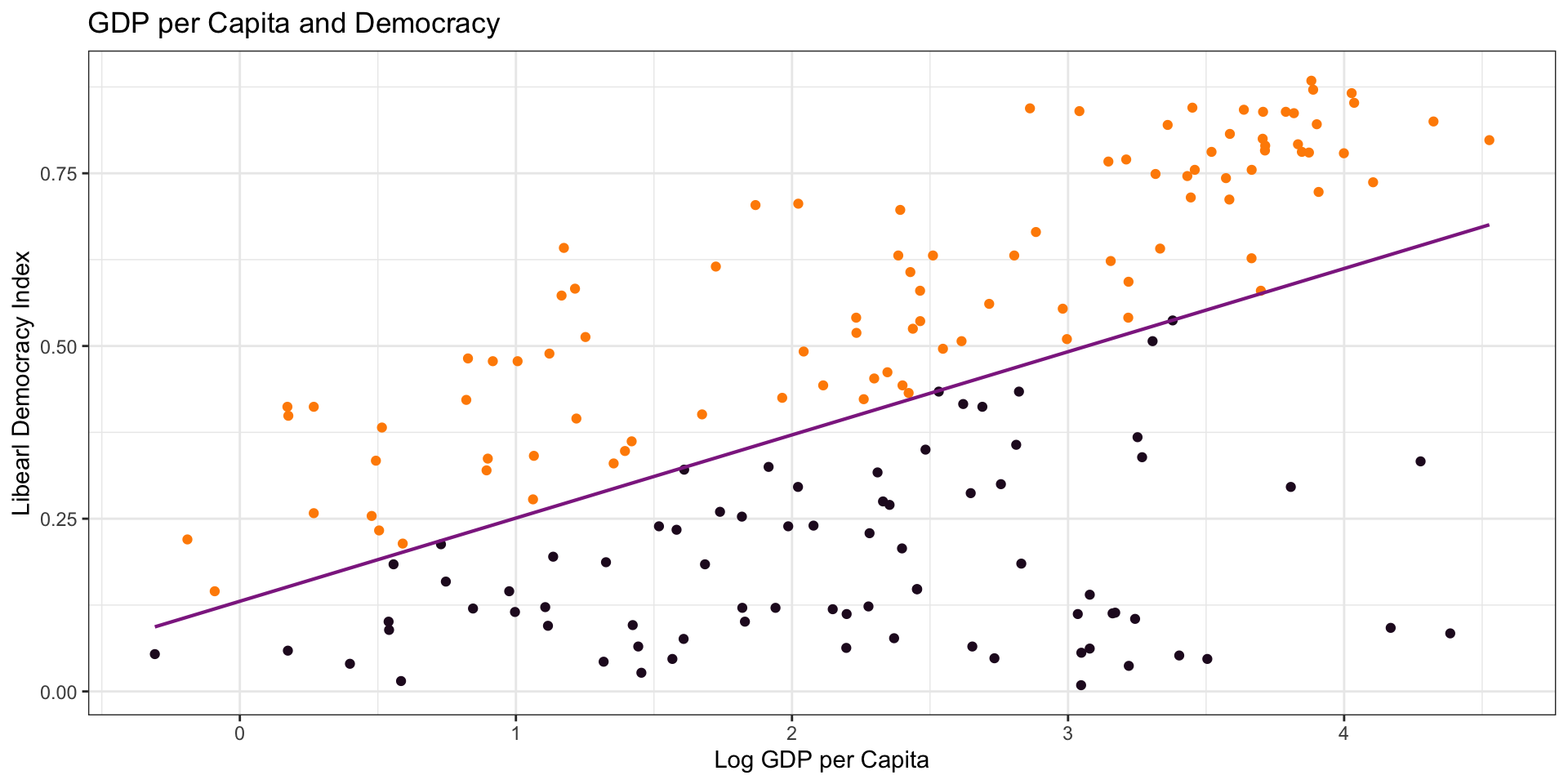
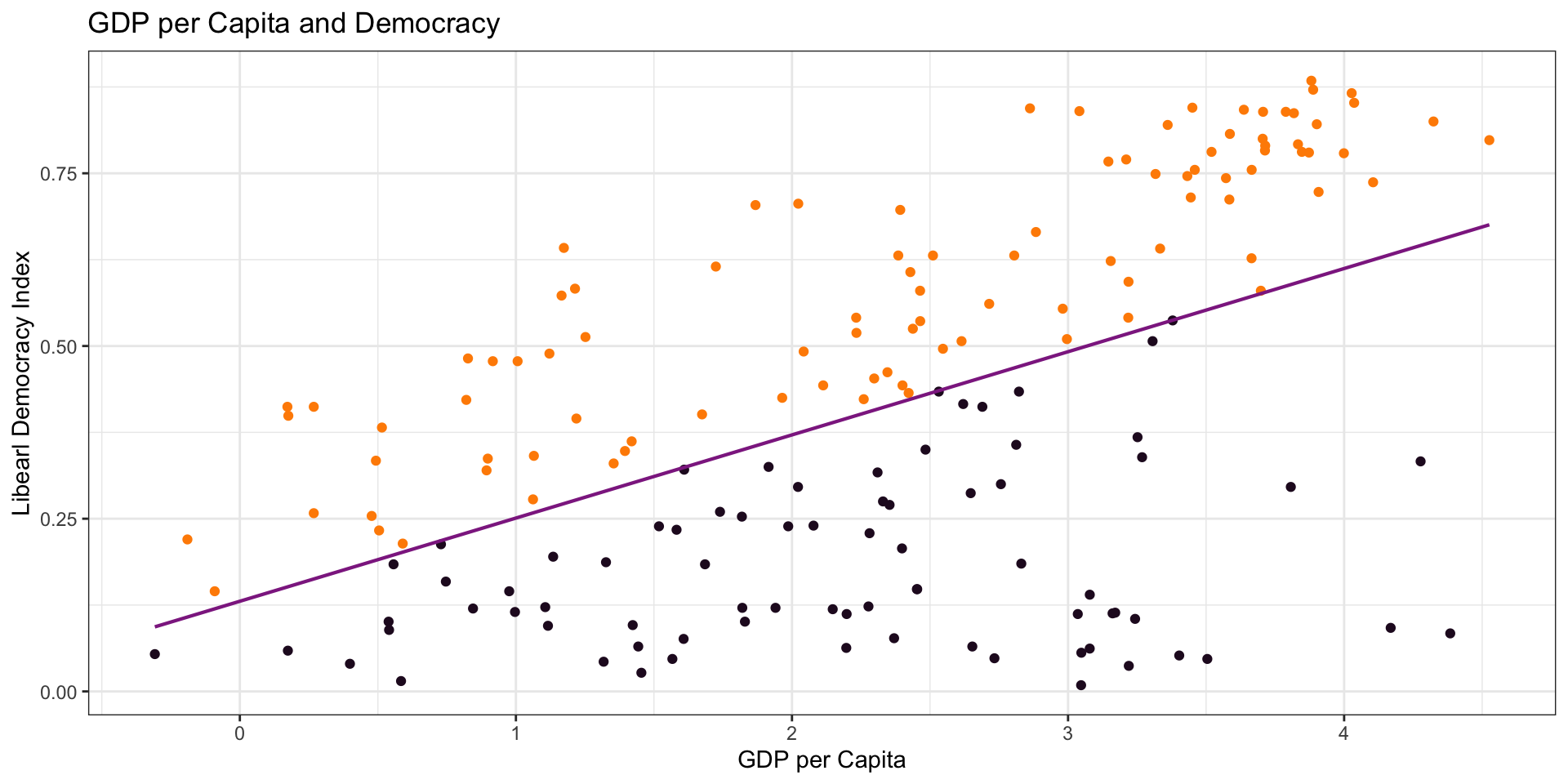
Example: GDP per capita and Democracy
Pull in the VDEM Data
Plot the Data
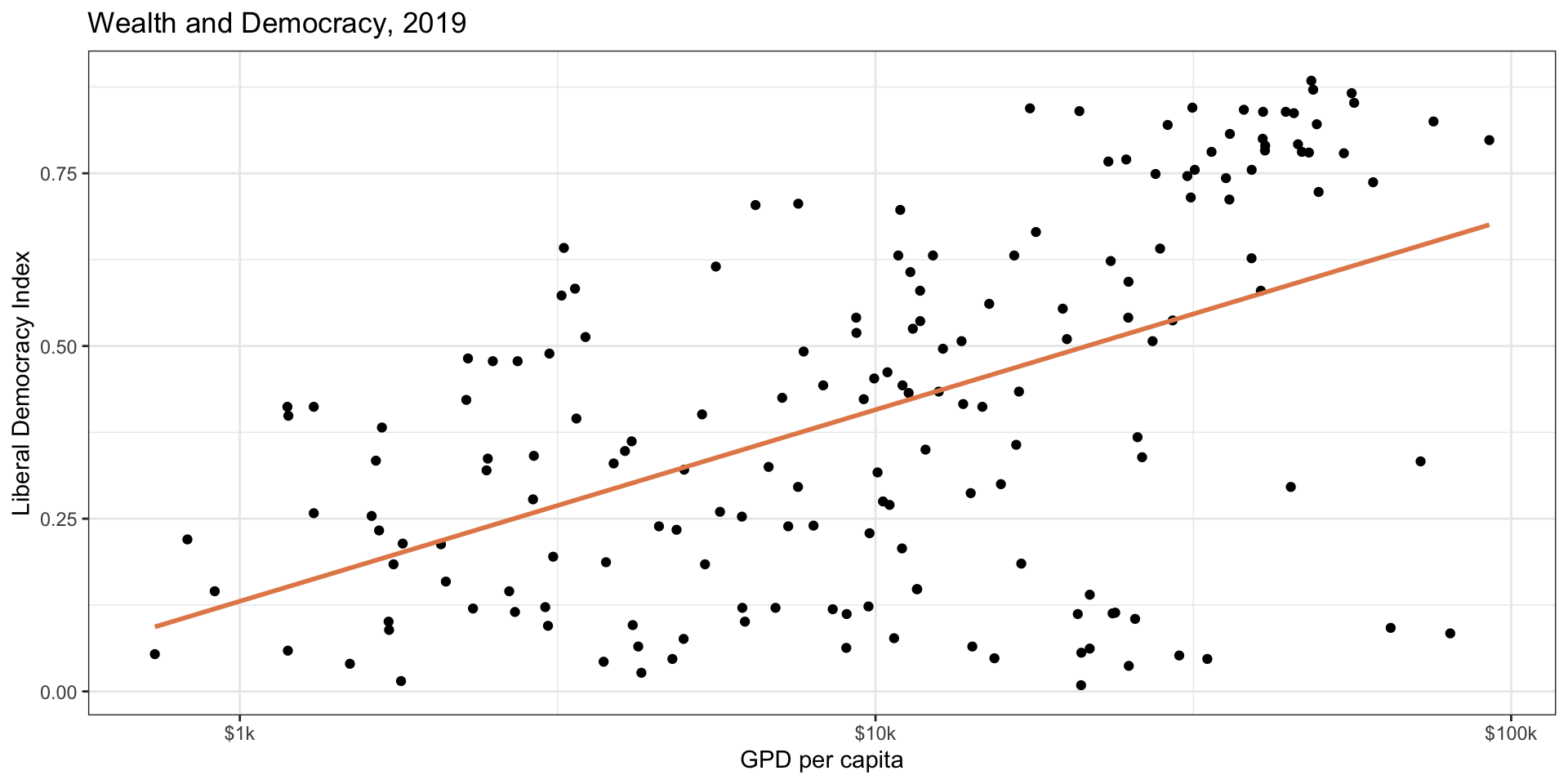
Plot the Data
Models as Functions
- We can represent relationships between variables using functions
- A function is a mathematical concept: the relationship between an output and one or more inputs
- Plug in the inputs and receive back the output
- Example: The formula \(y = 3x + 7\) is a function with input \(x\) and output \(y\).
- If \(x\) is \(5\), \(y\) is \(22\),
- \(y = 3 \times 5 + 7 = 22\)
Quant Lingo
- Response variable: Variable whose behavior or variation you are trying to understand, on the y-axis in the plot
- Dependent variable
- Outcome variable
- Y variable
- Explanatory variables: Other variables that you want to use to explain the variation in the response, on the x-axis in the plot
- Independent variables
- Predictors
Linear model with one explanatory variable…
- \(Y = a + bX\)
- \(Y\) is the outcome variable
- \(X\) is the explanatory variable
- \(a\) is the intercept: the predicted value of \(Y\) when \(X\) is equal to 0
- \(b\) is the slope of the line (rise over run)
Quant Lingo
- Predicted value: Output of the model function
- The model function gives the typical (expected) value of the response variable conditioning on the explanatory variables
- We often call this \(\hat{Y}\) to differentiate the predicted value from an observed value of Y in the data
- Residuals: A measure of how far each case is from its predicted value (based on a particular model)
- Residual = Observed value (\(Y\)) - Predicted value (\(\hat{Y}\))
- How far above/below the expected value each case is
Caution
Note that for the next few examples we will be analyzing GDP per capita on a log scale.
Residuals
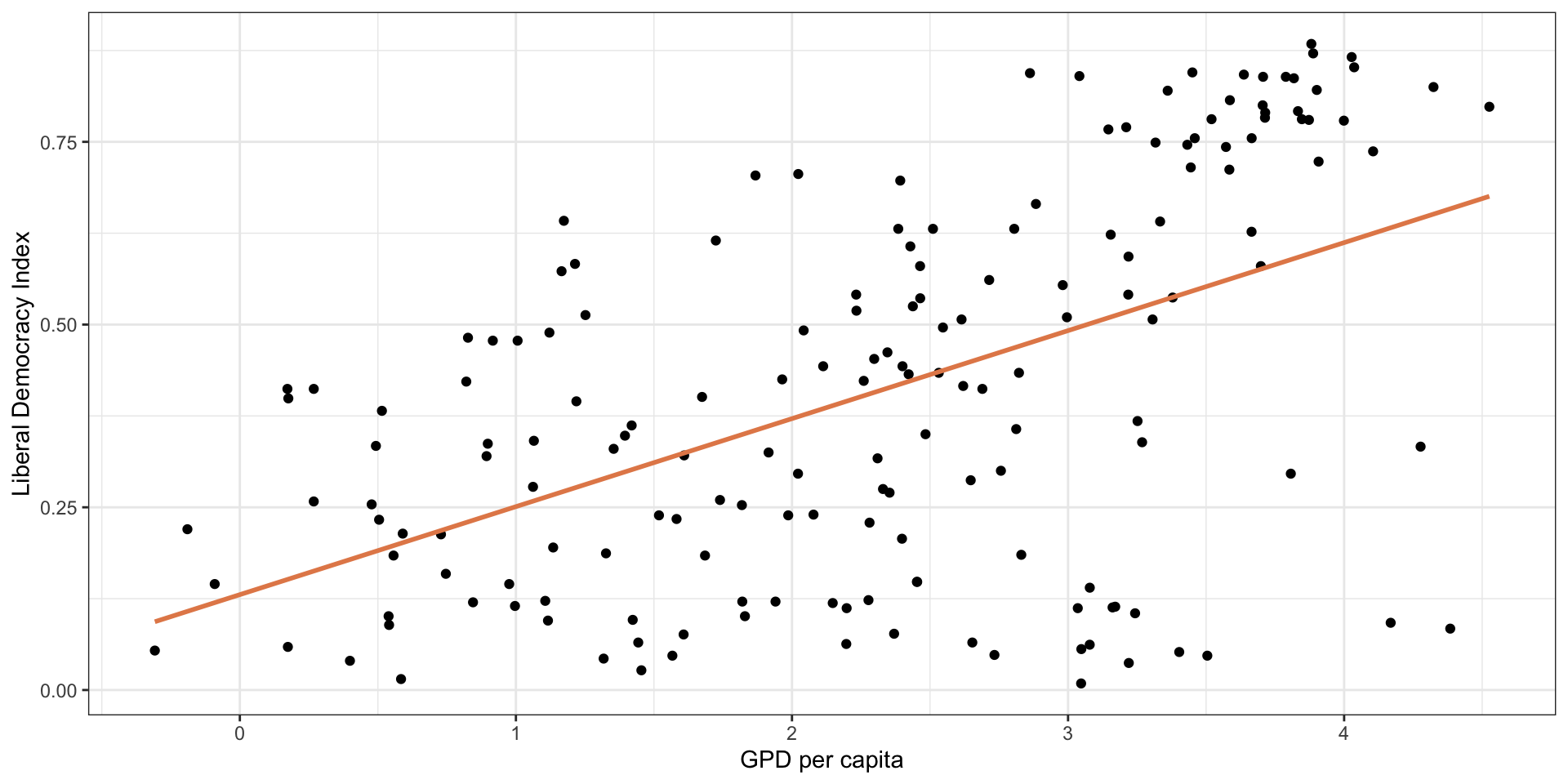
Linear Model
\(\hat{Y} = a + b \times X\)
\(\hat{Y} = 0.13 + 0.12 \times X\)
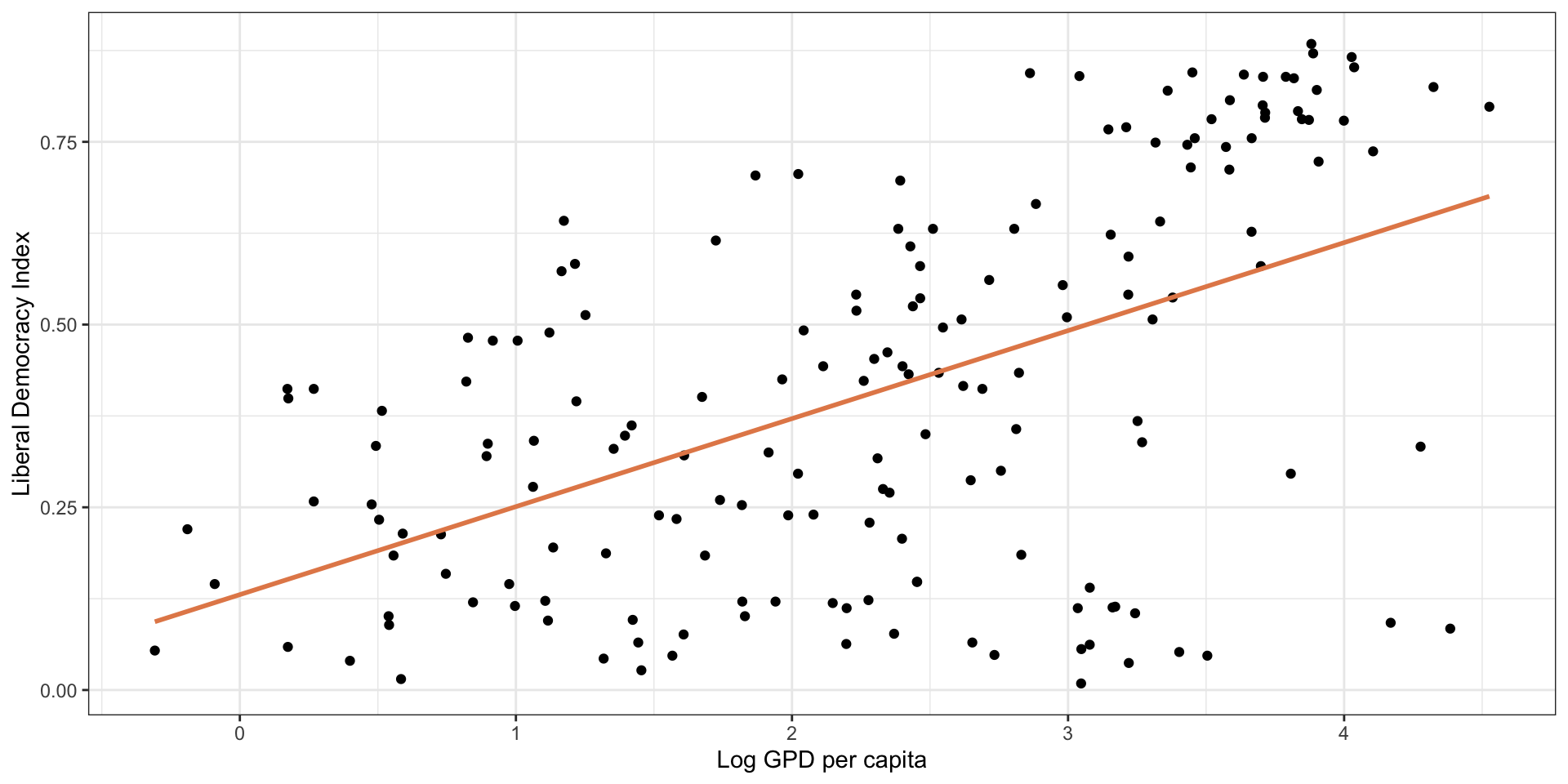
Linear Model: Interpretation
\(\hat{Y} = 0.13 + 0.12 \times X\)
What is the interpretation of our estimate of \(a\)?
\(\hat{Y} = 0.13\)
\(a\) is our predicted level of democracy when GDP per capita is 0.
Linear Model: Interpretation
\(\hat{Y} = 0.13 + 0.12 \times X\)
What is interpretation of our estimate of \(b\)?
\(\hat{Y} = a + \frac{Change Y}{Change X} \times X\)
Linear Model: Interpretation
\(0.12 = \frac{Change Y}{Change X}\)
\({Change Y} = 0.12 * {ChangeX}\)
\({Change Y = 0.12}\)
Linear Model: Interpretation
Linear Model: Interpretation
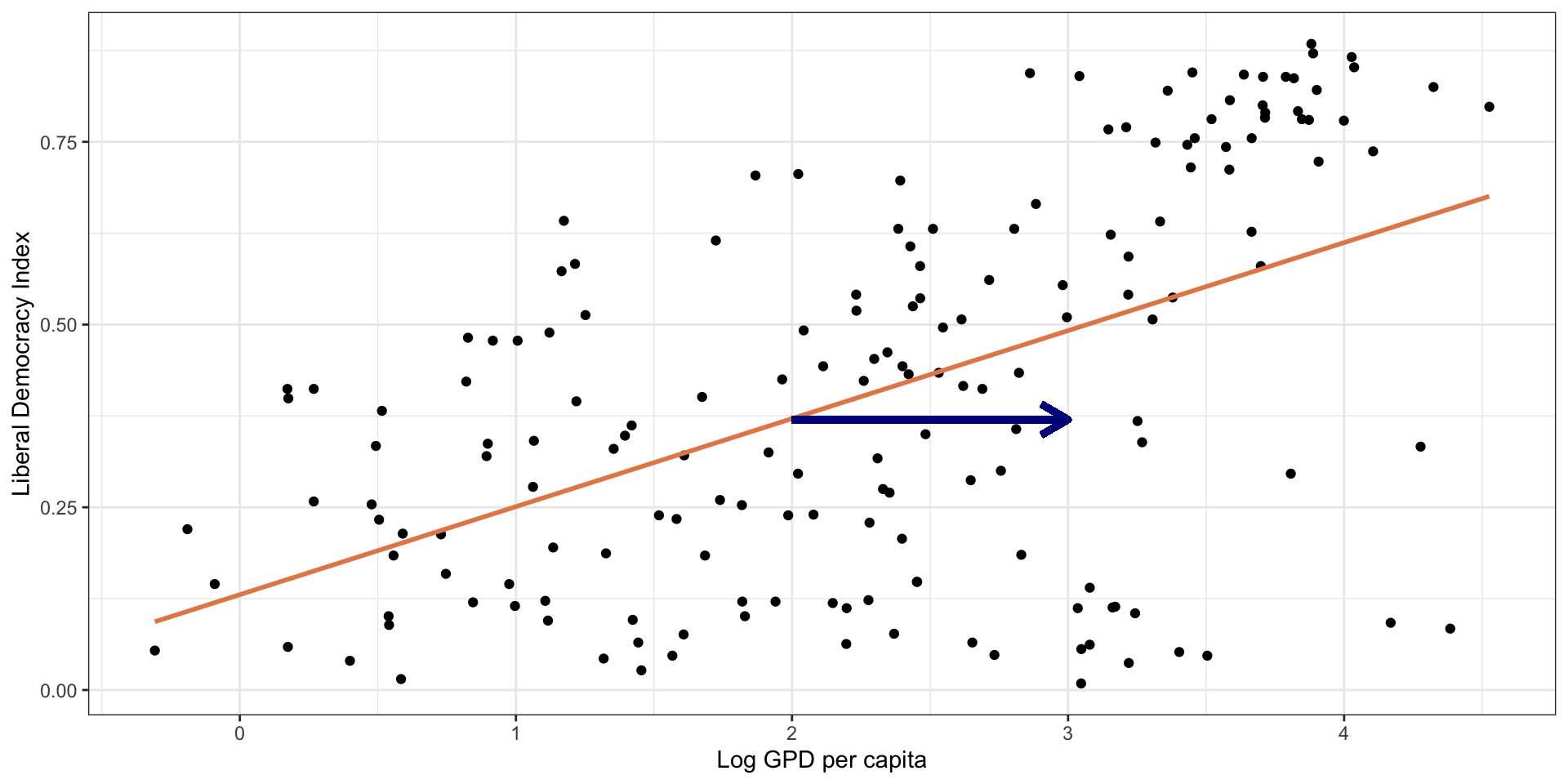
Linear Model: Interpretation
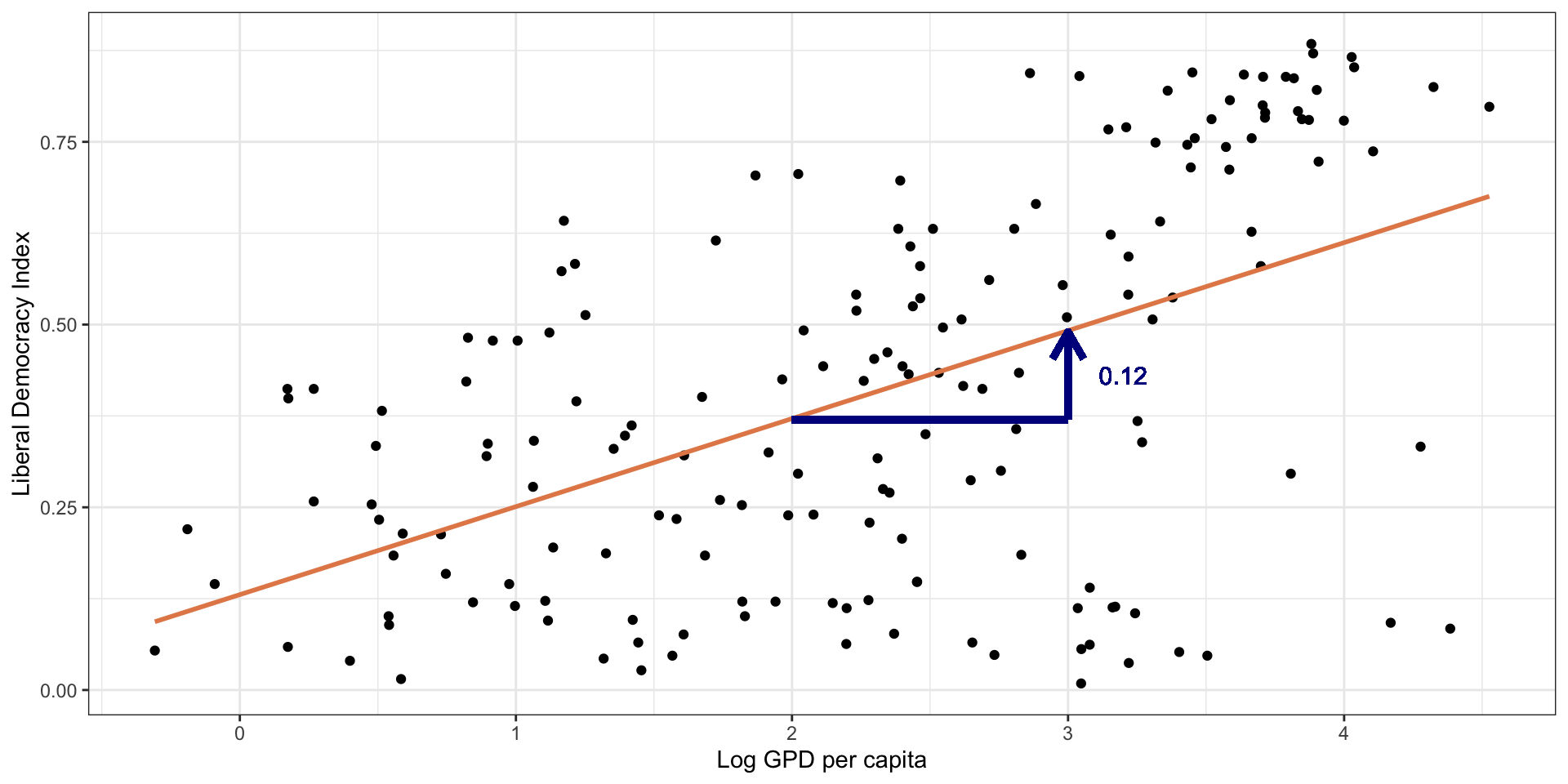
Interpreting the Coefficient for log(Wealth)
\[ \text{Democracy} = 0.12 \times \log(\text{Wealth}) \]
For small percentage changes in a “log-linear” model, we can use the approximation rule (divide by 100):
- A 1% increase in GDP per capita is associated with a 0.0012 point increase in the democracy score.
- Rule: \(0.12 / 100 = 0.0012\)
For Larger Changes We Log the Change
A 10% increase (e.g., from $10,000 to $11,000) increases the democracy score by 0.0114 points since:
\[ 0.12 \times \ln(1.1) \approx 0.12 \times 0.0953 = 0.0114 \]
Similarly…
Doubling GDP per capita (e.g., $10,000 → $20,000) increases the democracy score by:
\[ 0.12 \times \ln(2) \approx 0.12 \times 0.693 = 0.083 \]
Tripling GDP per capita (e.g., $10,000 → $30,000) increases the democracy score by:
\[ 0.12 \times \ln(3) \approx 0.12 \times 1.099 = 0.132 \]
Linear Model: Interpretation
Is this the causal effect of GDP per capita on liberal democracy?
No! It is only the association…
To identify causality we need other methods (beyond the scope of this course).
Your Task
An economist is interested in the relationship between years of education and hourly wages. They estimate a linear model with estimates of \(a\) and \(b\) as follows:
\(\hat{Y} = 9 + 1.60*{YrsEdu}\)
2. What is the predicted hourly wage for those with 10 years of education?
3. How about for those with a high school diploma? (12 yrs)
4. What about a college degree? (16 yrs)
Next step
- Linear model with one predictor: \(Y = a + bX\)
- For any given data…
- How do we figure out what the best values are for \(a\) and \(b\)??
Estimation
Linear Model with Single Predictor
Goal: Estimate Democracy score (\(\hat{Y_{i}}\)) of a country given level of GDP per capita (\(X_{i}\)).
Or: Estimate relationship between GDP per capita and democracy.
Linear Model with Single Predictor
Estimate Model
Call:
lm(formula = lib_dem ~ log_wealth, data = modelData)
Residuals:
Min 1Q Median 3Q Max
-0.57441 -0.14334 0.03911 0.18730 0.37017
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.13051 0.03806 3.429 0.000758 ***
log_wealth 0.12040 0.01471 8.188 5.75e-14 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.2233 on 172 degrees of freedom
(5 observations deleted due to missingness)
Multiple R-squared: 0.2805, Adjusted R-squared: 0.2763
F-statistic: 67.04 on 1 and 172 DF, p-value: 5.754e-14In equation form… How do we interpret the model?
\[\widehat{Democracy}_{i} = 0.13 + 0.12 * {loggdppc}_{i}\]
Question
How do we get the “best” values for the slope and intercept?
How would you draw the “best” line?
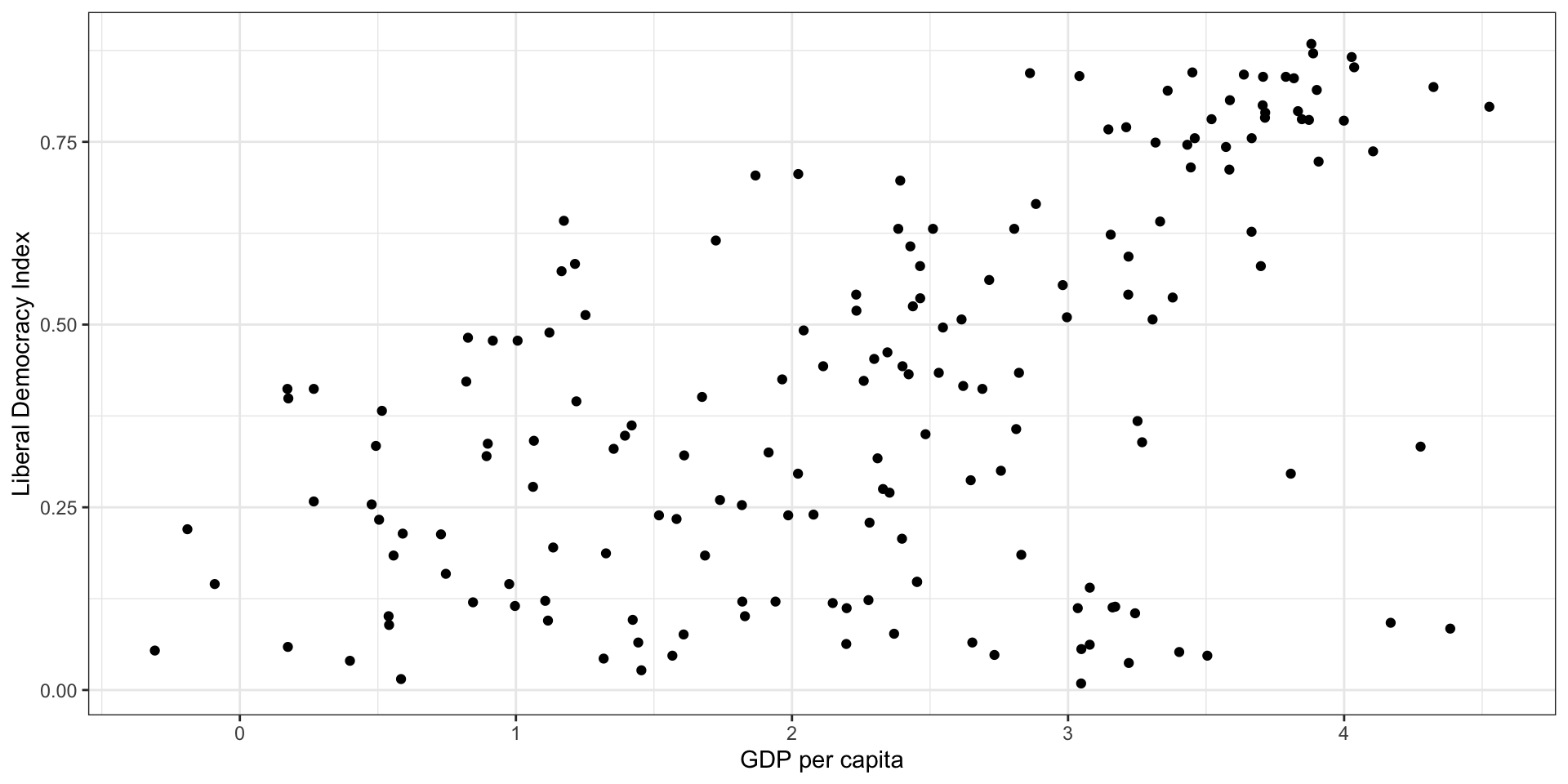
How would you draw the “best” line?
Least squares regression
- Remember the residual is the difference between the actual value and the predicted value
- The regression line minimizes the sum of squared residuals.
Least squares regression
Residual for each point is: \(e_i = y_i - \hat{y}_i\)
Least squares regression line minimizes \(\sum_{i = 1}^n e_i^2\).
- Why do we square the residual?
Why not take absolute value?
- Principle: larger penalty for residuals further away
- Math: makes the math easier and some nice properties (not our concern here…)
Least squares regression
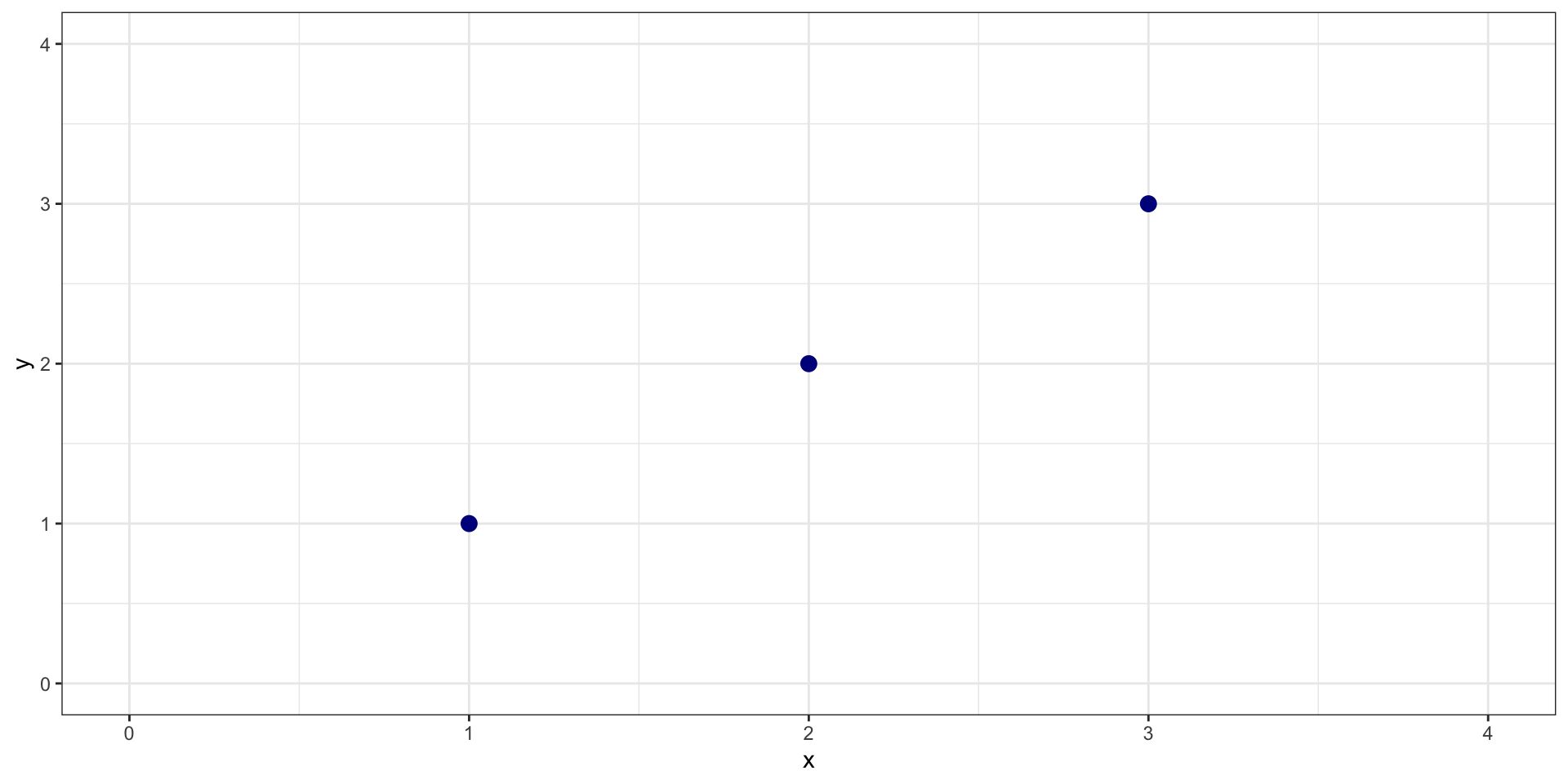
Very Simple Example
What should the slope and intercept be?
Example
\(\hat{Y} = 0 + 1*X\)
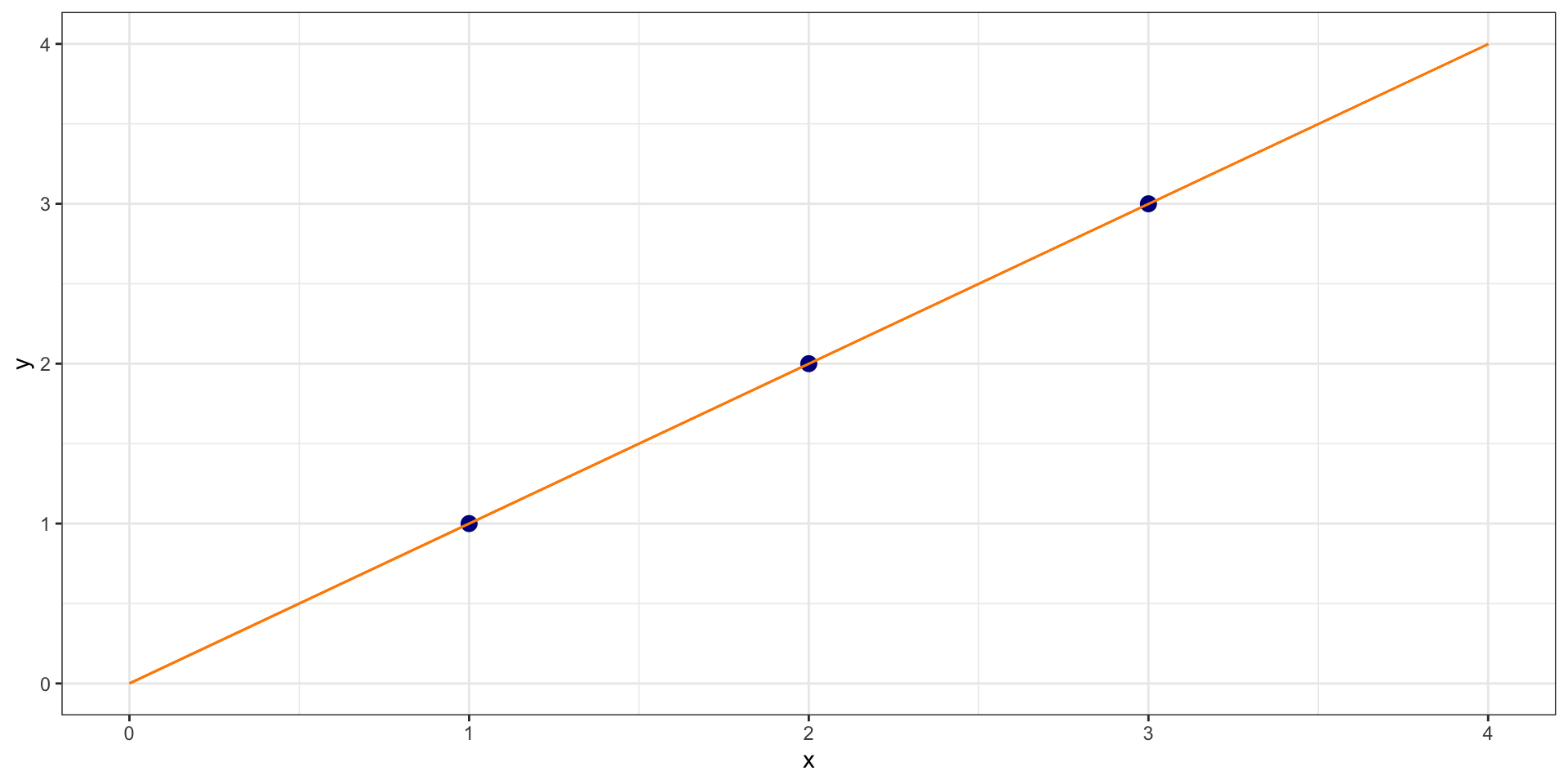
Example
What is the sum of squared residuals?
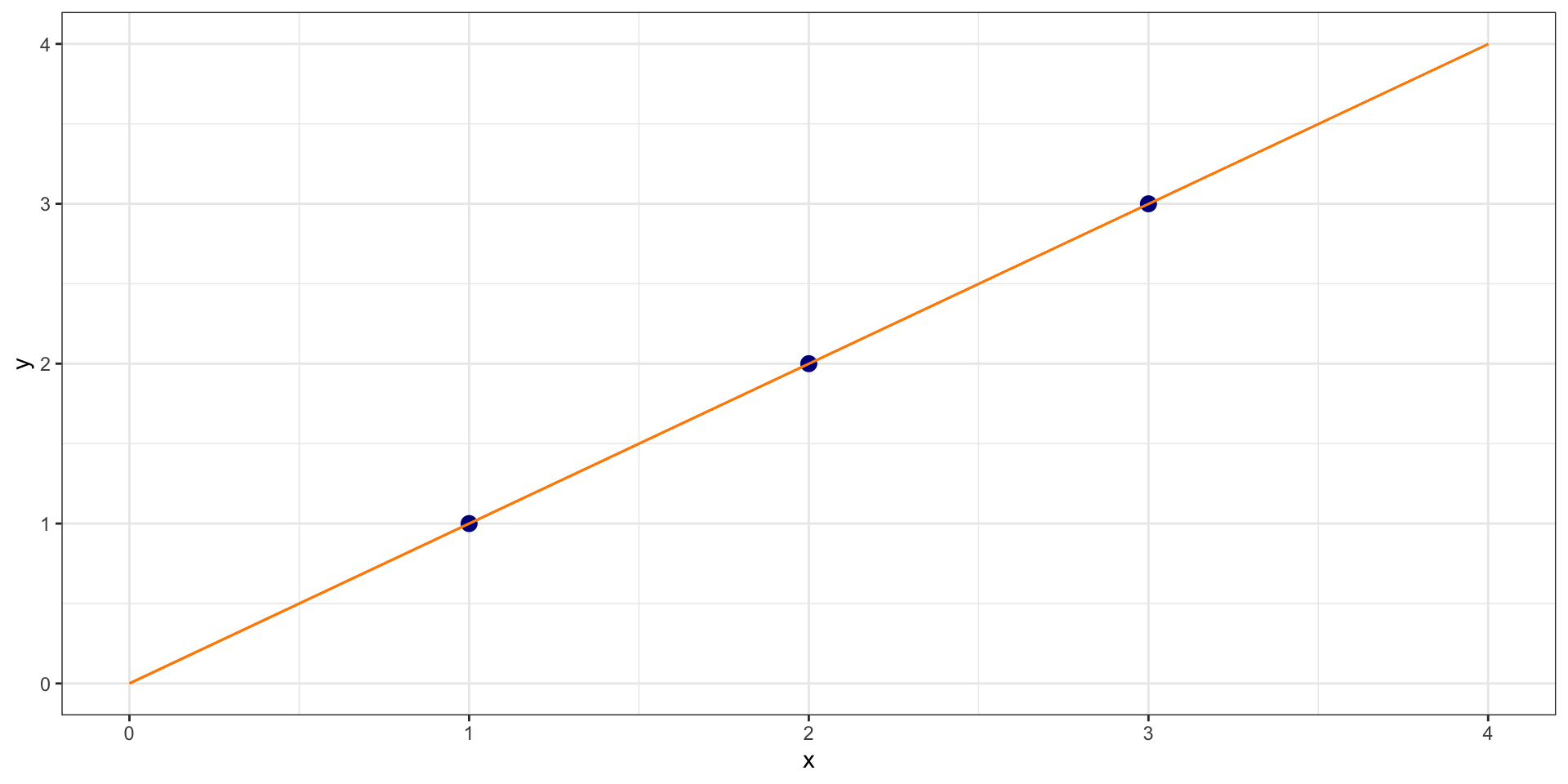
Example
What is sum of squared residuals for \(y = 0 + 0*X\)?
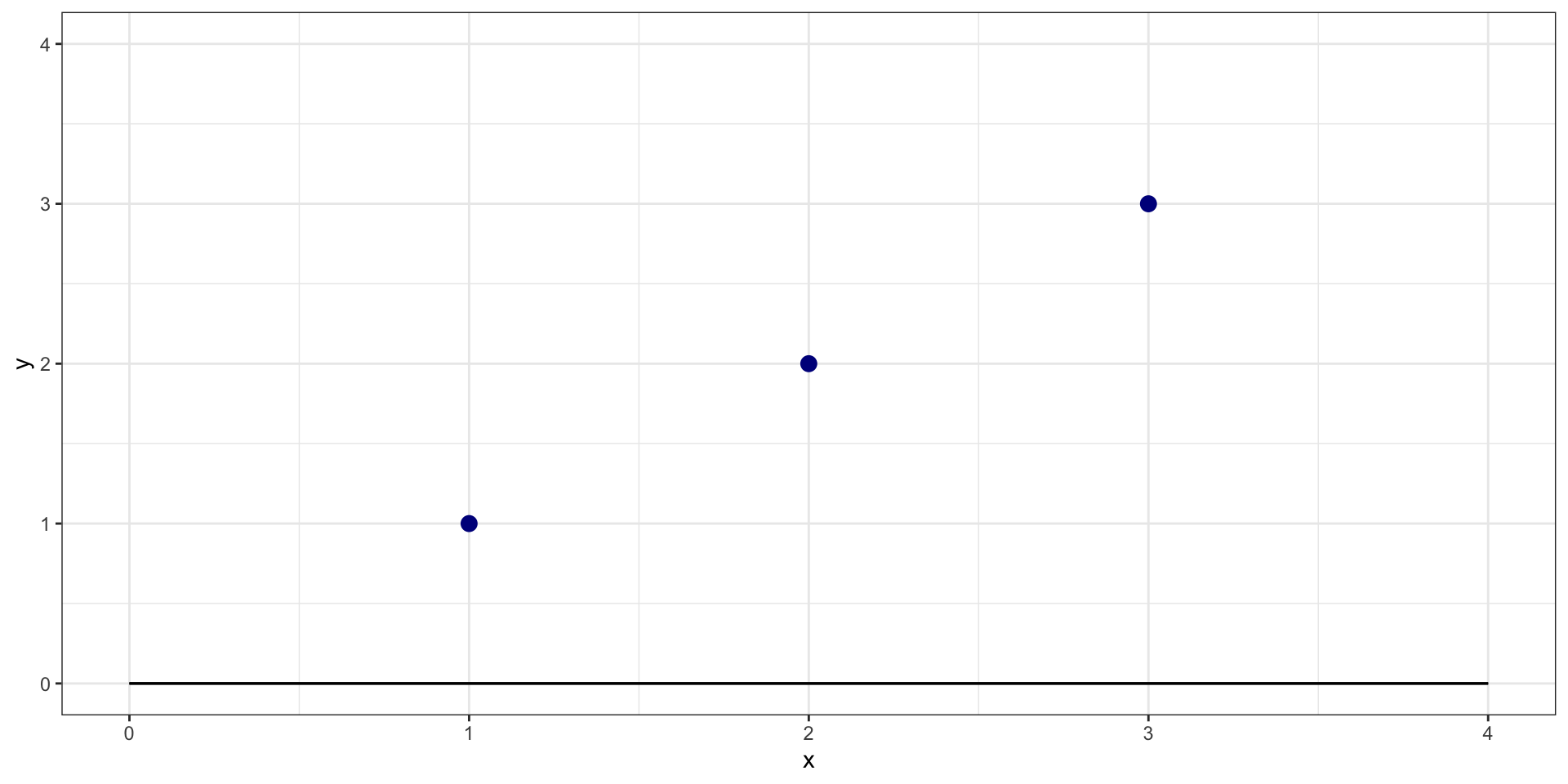
Example
What is sum of squared residuals for \(y = 0 + 0*X\)?
Example
What is sum of squared residuals for \(y = 0 + 2*X\)?
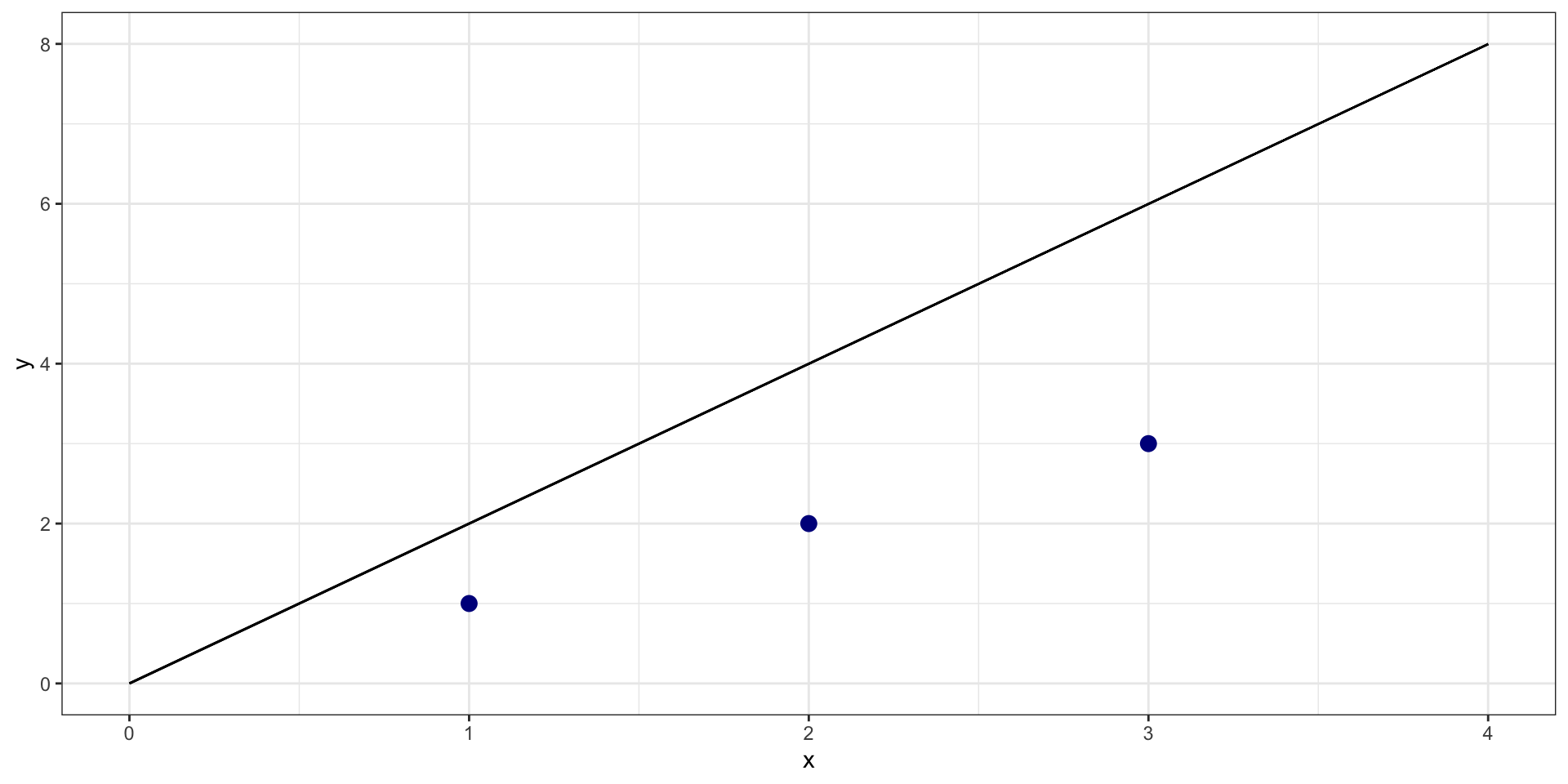
Example
What is sum of squared residuals for \(y = 0 + 2*X\)?
One more…
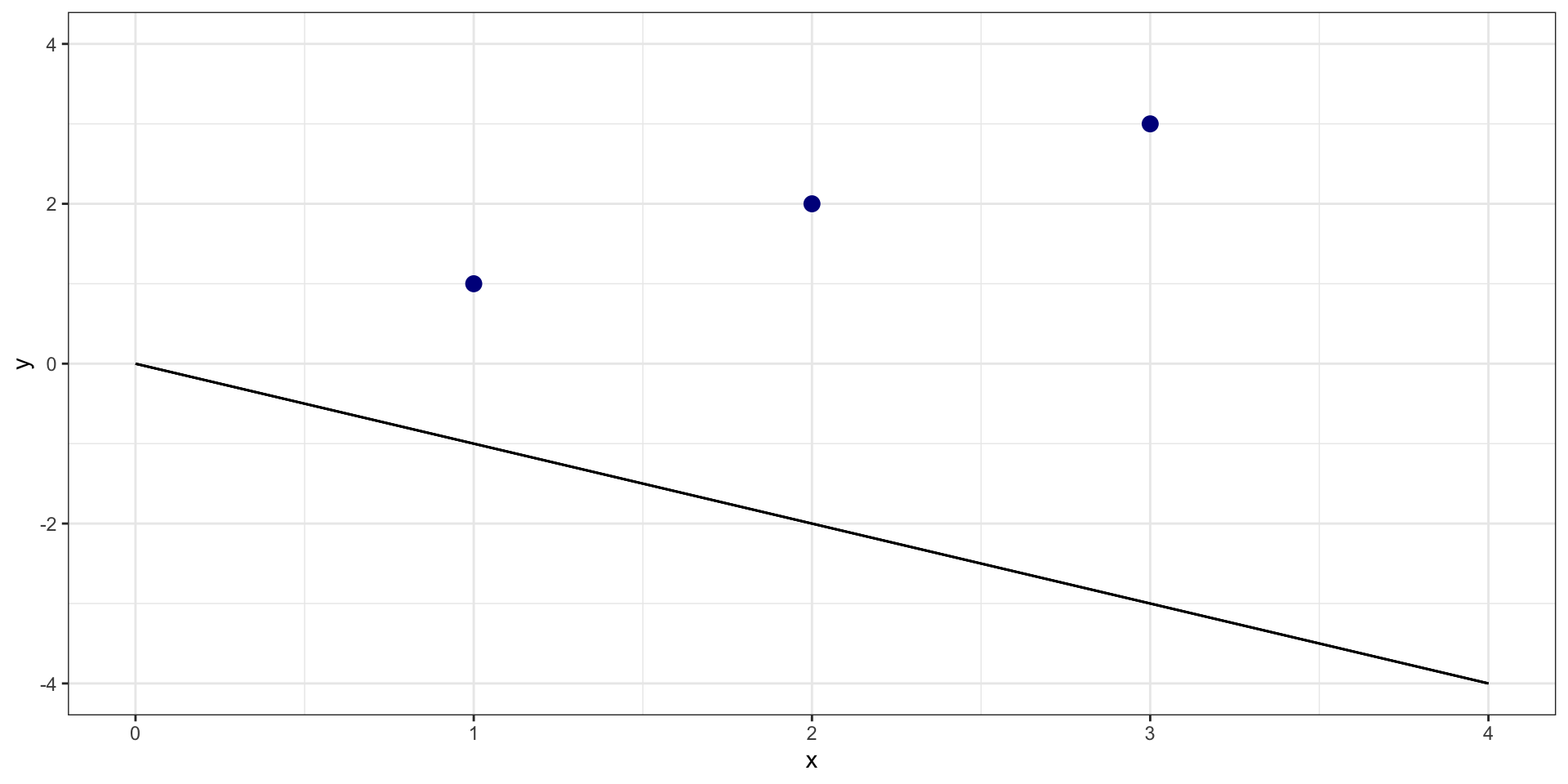
What is sum of squared residuals for \(y = 0 + -1*X\)?
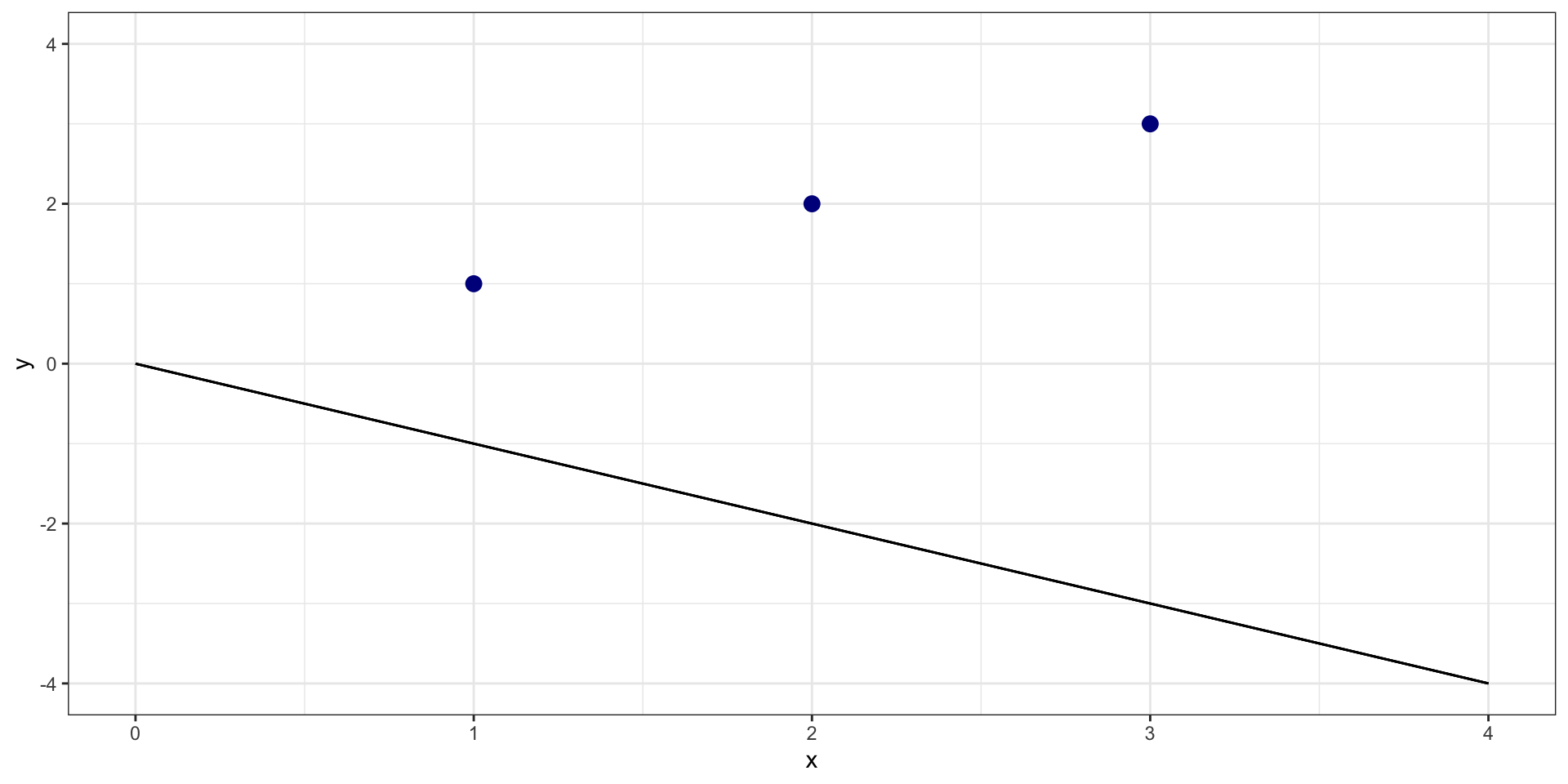
One more…
What is sum of squared residuals for \(y = 0 + -1*X\)?
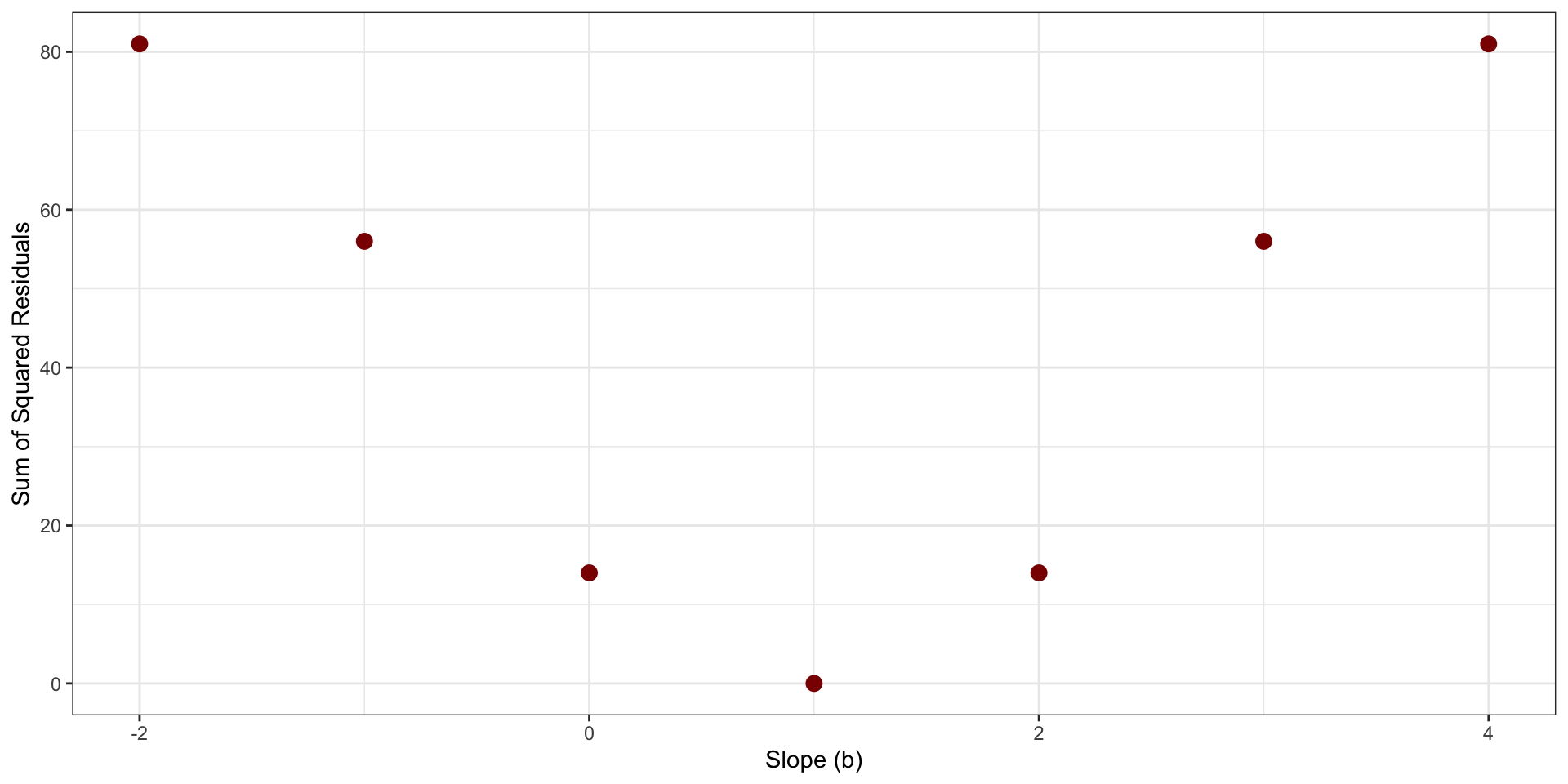
Cost Function
Sum of Squared Residuals as function of possible values of \(b\)
Least Squares Regression
When we estimate a least squares regression, it is looking for the line that minimizes sum of squared residuals
In the simple example, I set \(a=0\) to make it easier. More complicated when searching for combination of \(a\) and \(b\) that minimize, but same basic idea
Least Squares Regression
There is a way to solve for this analytically for linear regression (i.e., by doing math…)
– They made us do this in grad school…
- In machine learning, people also use gradient descent algorithm in which the computer searches over possible combinations of \(a\) and \(b\) until it settles on the lowest point.
Least Squares Regression
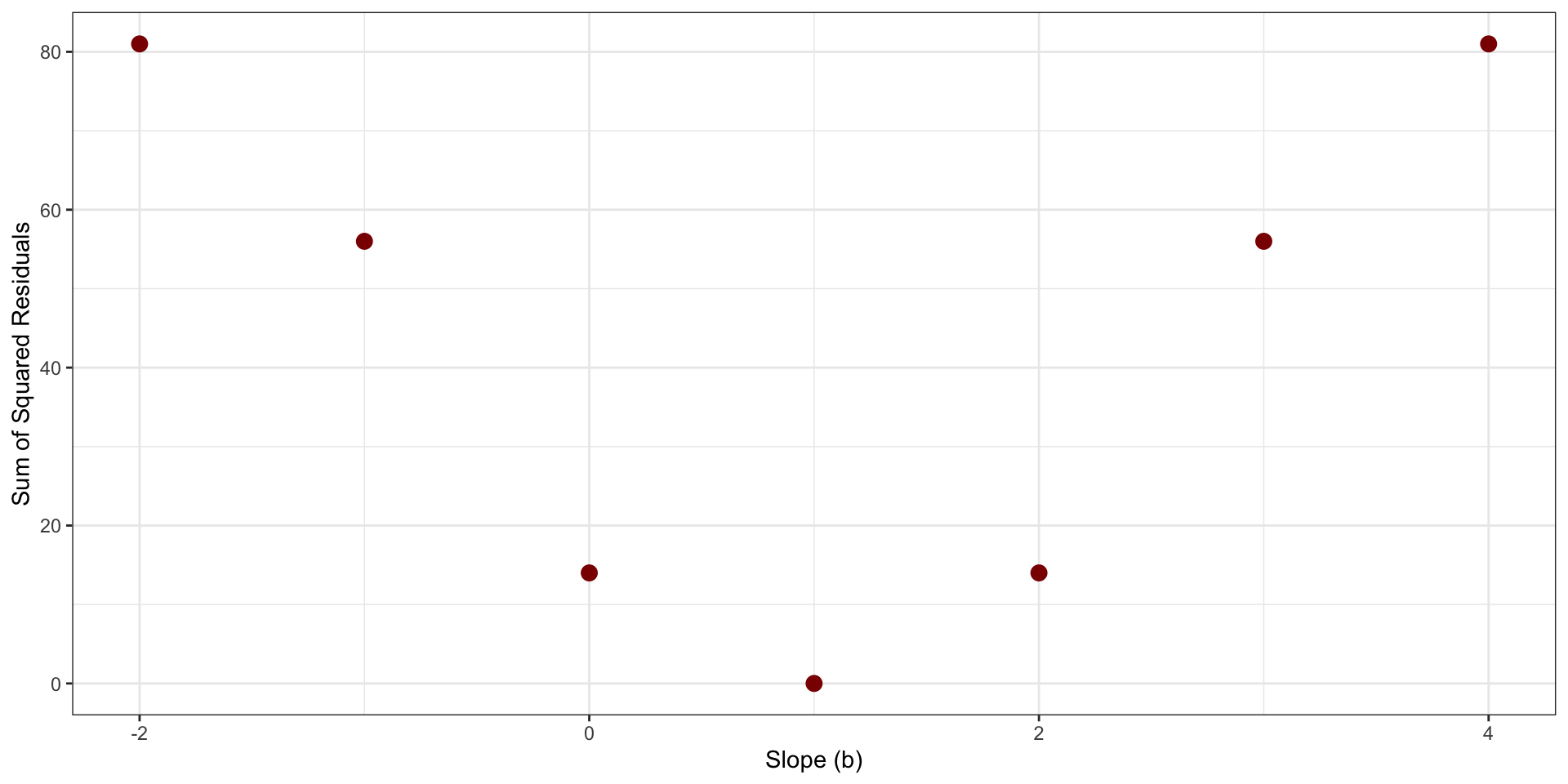
Least Squares Regression