Multiple Regression

October 21, 2024

Load packages


library(tidyverse)
library(vdemdata)

Load VDEM Data


model_data <- vdem |>
  filter(year == 2006) |> 
  select(country_name, 
         libdem = v2x_libdem, 
         wealth = e_gdppc, 
         oil_rents = e_total_oil_income_pc,
         polarization = v2cacamps, 
         corruption = v2x_corr, 
         judicial_review = v2jureview_ord, 
         region = e_regionpol_6C, 
         regime = v2x_regime) |> 
  mutate(
         region = factor(
           region,
           labels=c("Eastern Europe", 
             "Latin America", 
             "MENA", 
             "SSAfrica", 
             "Western Europe and North America", 
             "Asia and Pacific"))
          )

glimpse(model_data)

Linear Model with Multiple Predictors


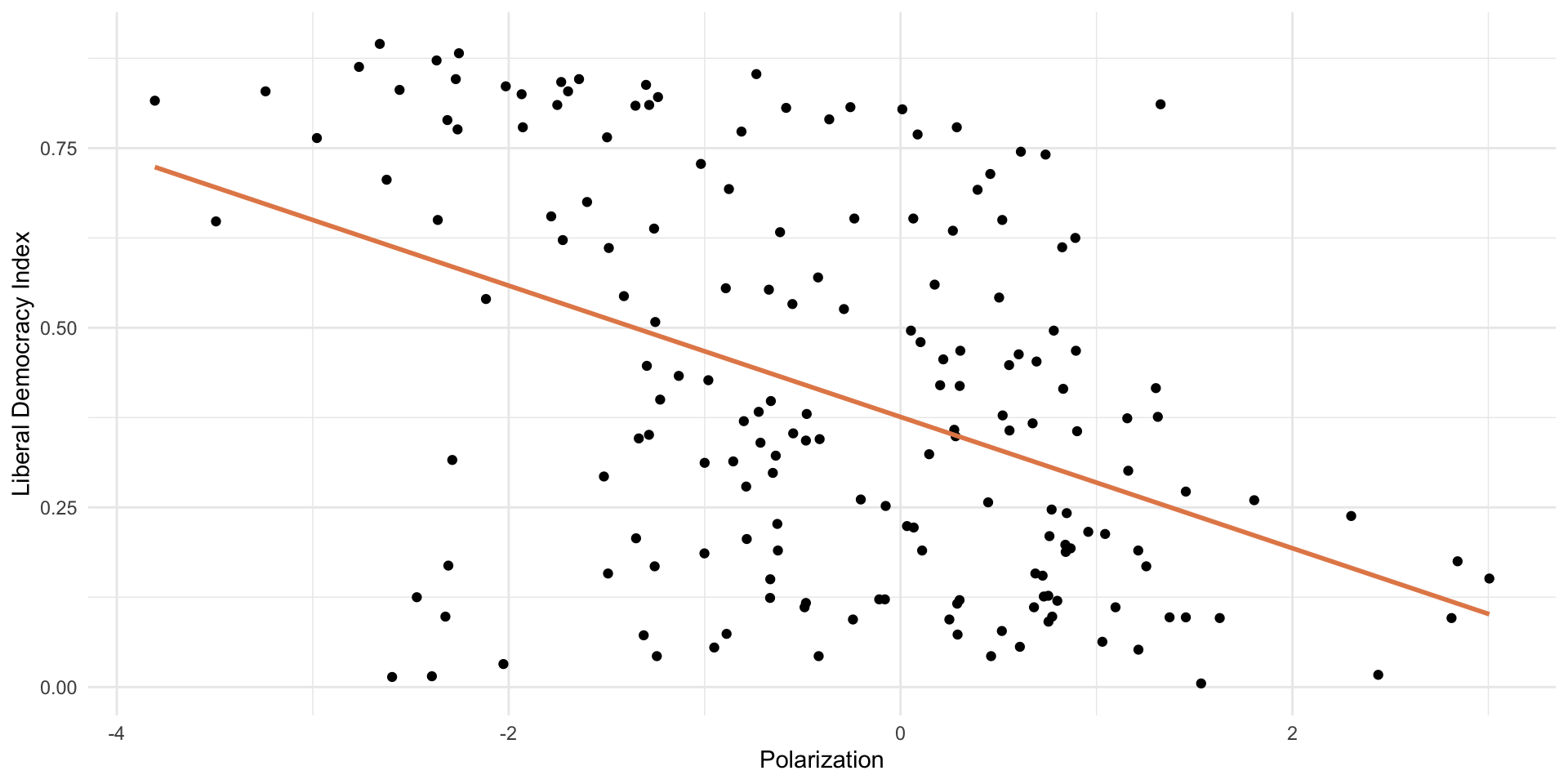
  • Previously, we were interested in GDP per capita as a predictor of democracy
  • Now, let’s consider another predictor: polarization (also measured by V-Dem)

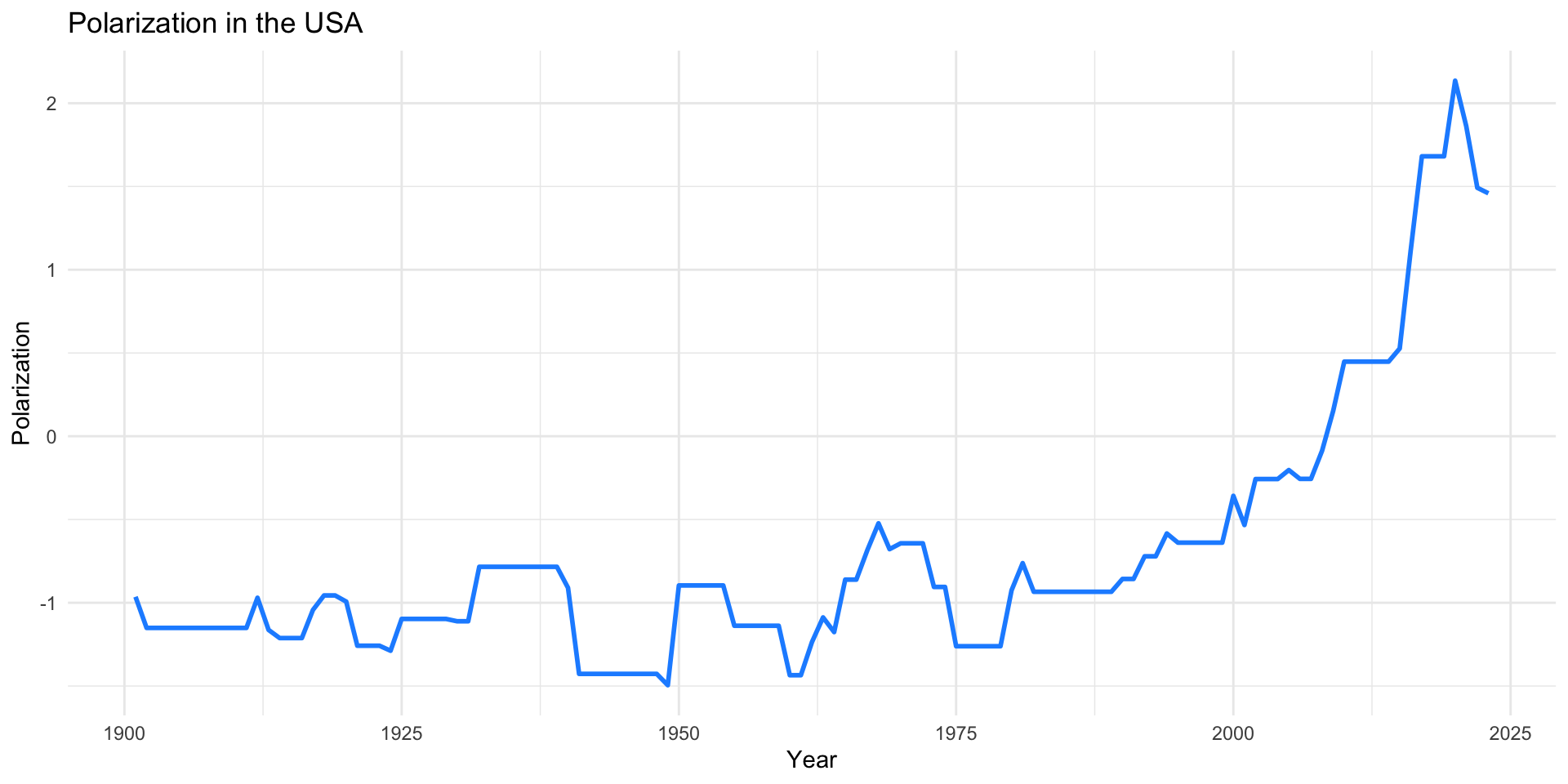
Polarization Measure in the USA

Polarization and Democracy in 2006

Model with One Predictor


library(broom) # for tidy() function

lm(libdem ~ polarization, data = model_data) |> 
  tidy() # for nicer regression output
# A tibble: 2 × 5
  term         estimate std.error statistic  p.value
  <chr>           <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    0.376     0.0187     20.1  2.66e-47
2 polarization  -0.0914    0.0139     -6.58 5.30e-10


How do we interpret the intercept and the slope estimate?
Significance?

Model with Two Predictors


lm(libdem ~ polarization + log(wealth), data = model_data) |> 
  tidy()
# A tibble: 3 × 5
  term         estimate std.error statistic       p.value
  <chr>           <dbl>     <dbl>     <dbl>         <dbl>
1 (Intercept)    0.196     0.0340      5.76 0.0000000390 
2 polarization  -0.0584    0.0138     -4.24 0.0000363    
3 log(wealth)    0.0944    0.0151      6.24 0.00000000334

Model with Two Predictors


\[ \hat{Y_i} = a + b_1*Polarization + b_2*GDPpc \]

\[ \hat{Y_i} = 0.18 + -0.05*Polarization + 0.10*GDPpc \]

Model with Two Predictors


\[ \hat{Y_i} = a + b_1*Polarization + b_2*GDPpc \]

\[ \hat{Y_i} = 0.18 + -0.05*Polarization + 0.10*GDPpc \]

\(a\) is the predicted level of Y when BOTH GDP per capita and polarization are equal to 0

Model with Two Predictors


\[ \hat{Y_i} = a + b_1*Polarization + b_2*GDPpc \]

\[ \hat{Y_i} = 0.18 + -0.05*Polarization + 0.10*GDPpc \]

  • \(b_1\) is the impact of a 1-unit change in polarization on the predicted level of Y, holding GDP per capita fixed (all else equal)
  • The relationship between polarization and democracy, controlling for wealth

Model with Two Predictors

\[ \hat{Y_i} = a + b_1*Polarization + b_2*GDPpc \]

\[ \hat{Y_i} = 0.18 + -0.05*Polarization + 0.10*GDPpc \]

  • \(b_2\) is the impact of a 1-unit change in GDP per capita on the predicted level of Y, holding polarization fixed (all else equal)
  • The relationship between wealth and democracy, controlling for polarization

Model with Two Predictors


\[ \hat{Y_i} = a + b_1*Polarization + b_2*GDPpc \]

  • OLS is searching for combination of \(a\), \(b_1\), and \(b_2\) that minimize sum of squared residuals
  • Same logic as model with one predictor, just more complicated

Model with Three Predictors


\[ \hat{Y_i} = a + b_1*Polarization + b_2*GDPpc + b_3*OilRents \]

Model with Three Predictors


lm(libdem ~ polarization + log(wealth) + oil_rents, data = model_data) |> 
  tidy()
# A tibble: 4 × 5
  term           estimate  std.error statistic  p.value
  <chr>             <dbl>      <dbl>     <dbl>    <dbl>
1 (Intercept)   0.153     0.0317          4.82 3.30e- 6
2 polarization -0.0577    0.0128         -4.50 1.32e- 5
3 log(wealth)   0.131     0.0150          8.72 3.65e-15
4 oil_rents    -0.0000413 0.00000607     -6.80 1.98e-10

Model with Three Predictors


\[ \hat{Y_i} = a + b_1*Polarization + b_2*GDPpc + b_3*OilRents \]

\[ \hat{Y_i} = a + -.05*Polarization + .13*GDPpc + .00004*OilRents \]

\(b_3\) is the impact of a 1-unit change in oil revenues per capita on the predicted level of Y, holding polarization and GDP fixed (all else equal)

Your Turn!


  • In the last session, you examined levels of democracy and corruption
  • Now, let’s fit a multiple regression model predicting corruption with two predictors: democracy (libdem) and polarization (polarization)
  • Then, interpret the coefficients
  • Estimate a second multiple regression model that adds in GDP per capita (lg_gdppc)
  • Interpret the coefficients
  • What happens to the coefficients of the other variables when we add GDP per capita to the model?
    • Why do you think this happens?
  • Try adding in additional predictors if there is time
10:00

Model 1


lm(corruption ~ libdem + polarization , data = model_data) |>
      tidy() 
# A tibble: 3 × 5
  term         estimate std.error statistic  p.value
  <chr>           <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    0.853     0.0267     32.0  9.12e-75
2 libdem        -0.780     0.0592    -13.2  6.16e-28
3 polarization   0.0459    0.0122      3.78 2.19e- 4

Model 2 - Adding GDP per capita


lm(corruption ~ libdem + polarization + log(wealth), data = model_data) |>
      tidy() 
# A tibble: 4 × 5
  term         estimate std.error statistic  p.value
  <chr>           <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)    0.962     0.0278     34.6  1.25e-78
2 libdem        -0.618     0.0574    -10.8  6.40e-21
3 polarization   0.0298    0.0108      2.75 6.66e- 3
4 log(wealth)   -0.0864    0.0125     -6.89 1.07e-10

Categorical Variables

What is a Categorical Variable?


  • A variable that represents distinct groups or categories
  • Categories can be named (e.g., “Male” or “Female”)
  • Or numbered (e.g., 1, 2, 3)
  • Or words (like different regions)
  • Can be either nominal (unordered) or ordinal (ordered)
  • Also called “dummy variables” or “indicator variables”

What is a Factor in R?


  • A data structure used to represent categorical variables
  • Can be dichotomous (binary) or have multiple levels
  • Supports both ordered and unordered categories
  • Call factor() to convert a variable to a factor
  • Call levels() to see the categories

Reference Categories


  • In a regression model, every categorical variable needs a reference category
  • The reference category is the category that all other categories are compared to when interpreting the results
  • Call relevel() to change the reference category

Judicial Review and Democracy


Judicial Review:

  • Do high courts (Supreme Court, Constitutional Court, etc) have the power to rule on whether laws or policies are constitutional/legal? (Yes or No)
  • Dimension of Judicial Independence

Judicial Review and Democracy

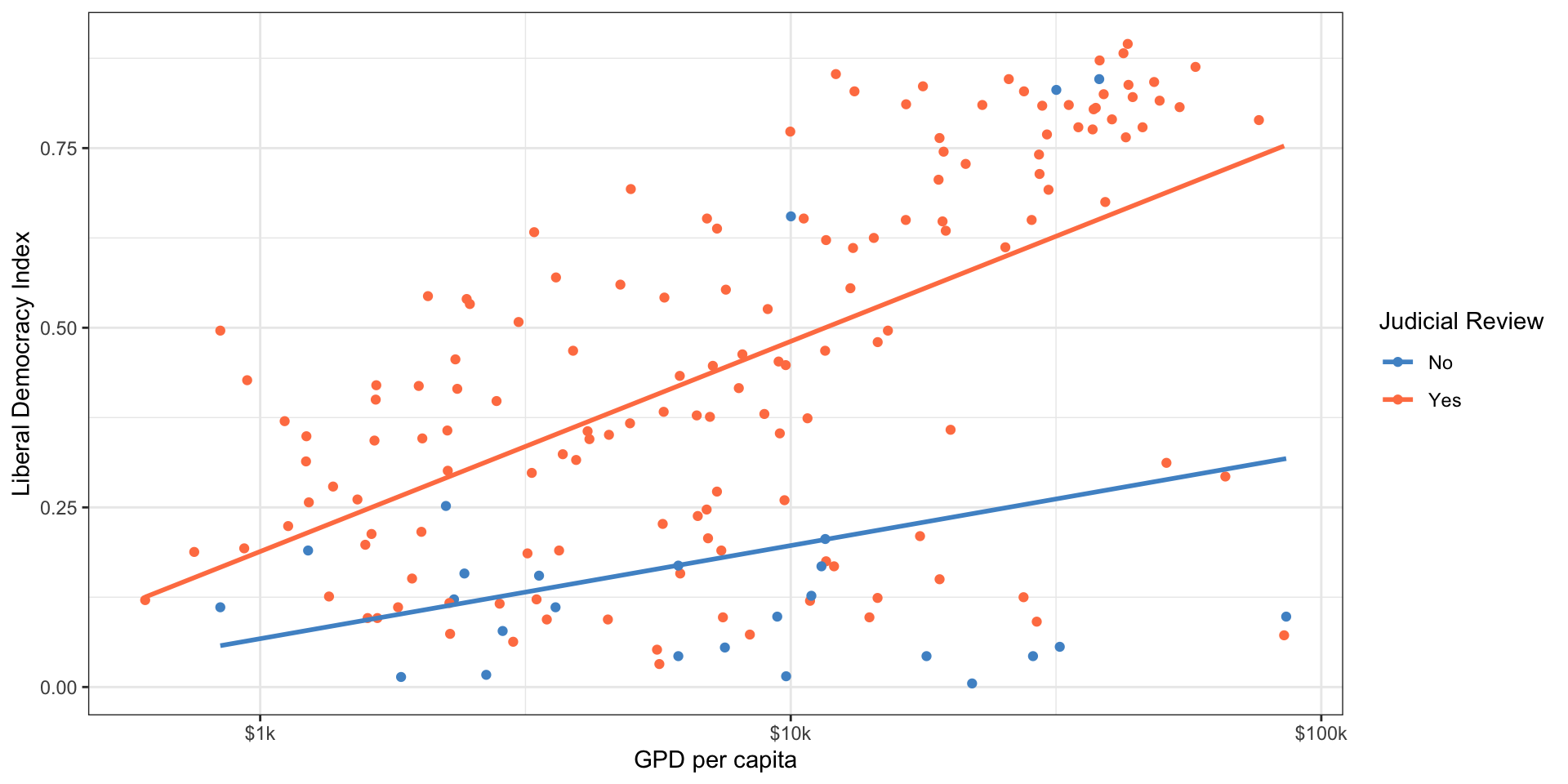
Judicial Review and Democracy


lm(libdem ~ factor(judicial_review), data = model_data) |>
  tidy()
# A tibble: 2 × 5
  term                     estimate std.error statistic    p.value
  <chr>                       <dbl>     <dbl>     <dbl>      <dbl>
1 (Intercept)                 0.179    0.0493      3.64 0.000355  
2 factor(judicial_review)1    0.267    0.0533      5.01 0.00000130

Judicial Review and Democracy


\[ \widehat{Democracy_{i}} = 0.17 + 0.28*JudicialReview(yes) \]

  • Slope: countries with judicial review are expected, on average, to be 0.28 units more democratic on the liberal democracy index
    • Compares baseline level (Judicial Review = 0) to the other level (Judicial Review = 1)
  • Intercept: average democracy score of countries without judicial review
  • Average democracy score of countries with judicial review is 0.17 + 0.28 = 0.45

Dummy Variables


  • When the categorical explanatory variable has many levels, they’re encoded to dummy variables
  • We always leave one category out of the model, as the omitted reference category
  • Each coefficient describes is the expected difference between level of the factor and the baseline level
  • Everything is relative to the omitted reference category

Democracy and World Region


  • Does region predict levels of democracy?
  • Since Eastern Europe is the first category, default in R is to use that as the omitted category in models.
levels(model_data$region)
[1] "Eastern Europe"                   "Latin America"                   
[3] "MENA"                             "SSAfrica"                        
[5] "Western Europe and North America" "Asia and Pacific"

Democracy and World Region


How should we interpret intercept? How about the coefficient on Latin America?


lm(libdem ~ region, data = model_data) |>
  tidy()
# A tibble: 6 × 5
  term                                   estimate std.error statistic  p.value
  <chr>                                     <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)                              0.434     0.0361     12.0  1.41e-24
2 regionLatin America                      0.0664    0.0535      1.24 2.16e- 1
3 regionMENA                              -0.236     0.0571     -4.13 5.63e- 5
4 regionSSAfrica                          -0.139     0.0456     -3.06 2.61e- 3
5 regionWestern Europe and North America   0.376     0.0541      6.94 7.84e-11
6 regionAsia and Pacific                  -0.134     0.0519     -2.57 1.09e- 2

Democracy and World Region


What if you want a different baseline category? How do we interpret now?


# make SS Africa the reference category
model_data <- model_data |> 
mutate(newReg = relevel(region, ref=4)) 

lm(libdem ~ newReg, data = model_data) |>
      tidy()
# A tibble: 6 × 5
  term                                   estimate std.error statistic  p.value
  <chr>                                     <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)                             0.295      0.0279    10.6   2.24e-20
2 newRegEastern Europe                    0.139      0.0456     3.06  2.61e- 3
3 newRegLatin America                     0.206      0.0484     4.25  3.47e- 5
4 newRegMENA                             -0.0962     0.0523    -1.84  6.74e- 2
5 newRegWestern Europe and North America  0.515      0.0491    10.5   3.36e-20
6 newRegAsia and Pacific                  0.00582    0.0466     0.125 9.01e- 1

Your Turn


Which types of regime have more corruption?


V-Dem also includes a categorial regime variable: Closed autocracy (0), Electoral Autocracy (1), Electoral Democracy (2), Liberal Democracy (3)

Your Turn


Which types of regime have more corruption?


First, let’s make this an easier factor variable to work with.

# Make nicer regime factor variable
model_data <- model_data |> 
  mutate(regime = factor(regime,
                         labels = c("Closed Autocracy",
                                   "Electoral Autocracy",
                                  "Electoral Democracy",
                                  "Liberal Democracy")))
levels(model_data$regime)
[1] "Closed Autocracy"    "Electoral Autocracy" "Electoral Democracy"
[4] "Liberal Democracy"

Your Turn


Which types of regime have more corruption?


  • Filter data to include only the year 2019 (or run the code to use model_data)
  • Make a plot to visualize the relationship between regime type and level of corruption. - Which kind of plot is best in this situation?
  • Fit a linear model
  • Interpret the intercept and coefficients
10:00

Visualization

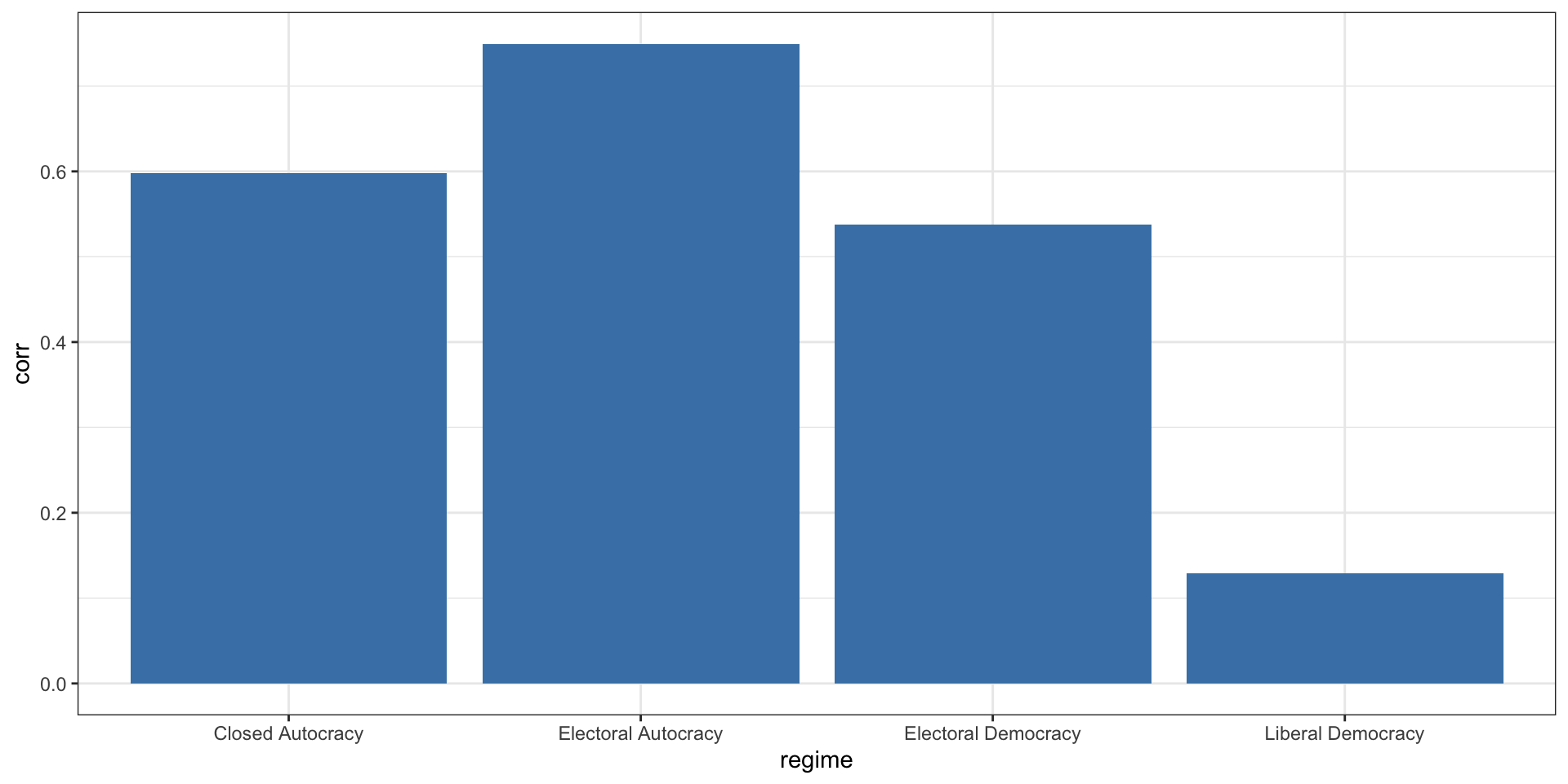
Model


lm(corruption ~ regime, data = model_data) |>
      tidy()
# A tibble: 4 × 5
  term                      estimate std.error statistic  p.value
  <chr>                        <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)                 0.598     0.0397     15.1  2.81e-33
2 regimeElectoral Autocracy   0.151     0.0475      3.18 1.74e- 3
3 regimeElectoral Democracy  -0.0606    0.0484     -1.25 2.11e- 1
4 regimeLiberal Democracy    -0.469     0.0502     -9.35 4.46e-17

Create Your Own Model


  • What is a theory that you would like to test with V-Dem data?
  • What is the dependent variable?
  • What are the independent variables?
  • Map out steps to wrangle the data and fit a regression model
  • What do you expect to find?
  • Now go ahead and wrangle the data
  • Fit the model
  • Interpret the coefficients and their significance
  • Did the results match your expectations?